Next Generation counters are up and running!

Software Heritage is archiving hundreds of millions of repositories, produced by tens of millions of developers. This amount to billions of distinct software artefacts (files, directories, revisions, releases) that need to be properly ingested in the gigantic Merkle graph that lies at the core of the archive.

It is quite natural to want to know how many artifacts are in the archive, from how many projects, and involving how many contributors: to answer these questions, we show a variety of counters on the main archive.

Counting billions of objects…

Maintaining these counters up to date may seem a no brainer, but when one looks at the details, it is not. Querying the database each time the main page is shown provides precise results, but involves a significant amount of interaction with the database, takes time, and puts unreasonable strain on the database.
A better approach seem for each loader to increment the global counters with the number of new objects it encounters. Unfortunately, if several workers happen to ingest forks of a same new project (and it does happen!), then the new objects end up being counted multiple times, and over time the counters diverge arbitrarily from the real values, so this is also a dead end.

… using probabilistic algorithms…

But let’s look at the gist of the idea: we have a stream of objects encountered by the loaders (possibly repeated), and we want to count the number of objects without repetition.

This problem has a precise definition in Mathematics: we are looking for the “cardinality of the support set of a multiset”. Also known as the “count distinct problem”, it has got a lot of attention from experts in Algorithms, in particular from Philippe Flajolet and his collaborators.

In particular, the seminal 2007 article “HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm” by Philippe Flajolet, Éric Fusy, Olivier Gandouet and Frédéric Meunier in Discrete Mathematics & Theoretical Computer Science, shows how to estimate cardinalities in the billions with accuracy of 1%, using a few kB of memory. This approach has gained broad popularity over the years, and there are now many well engineered implementations available.

… is now deployed

We have chosen to use the redis implementation due to the simplicity of its API and its robustness.
The global picture of the architecture is the following:

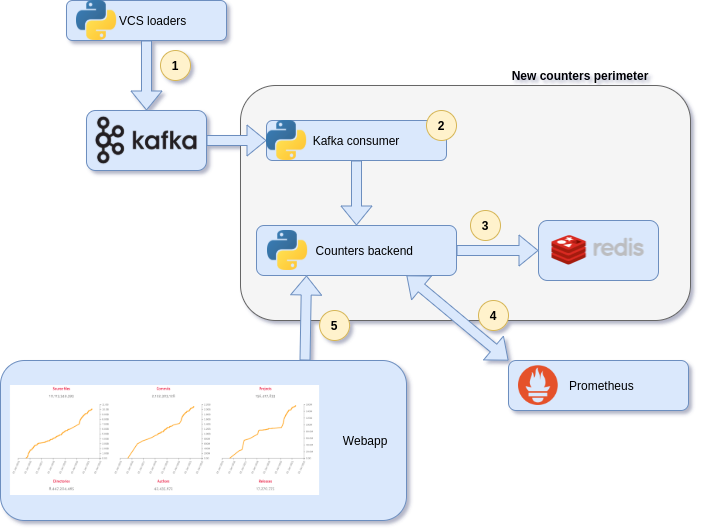
1. Several loaders are scrapping the repositories and populate several kafka topics, one per different object type (contents, directories, revisions, origins, …). They are mostly the objects we want to count
2. A kafka consumer reads the different topics and send by batch the kind of object and their keys to the counters backend
3. The backend creates an hyperloglog key per object type and counts the object’s unique keys with PFADD instructions, using a redis pipeline for more efficiency
4. A prometheus exporter periodically reads the counters value and stores them in timeseries in prometheus. The counters backend reads the timeseries every 4 hours and generates a json that will be used by the webapp to display the historical graphics
5. The webapp retrieves the live numbers and the historical data from the counters backend and renders them on the homepage

We can use an Hyperloglog key per object type because even if the number of objects to count is huge, each key is only using 12k bytes. We are able to count more than 20 billions of objects in 120k bytes!

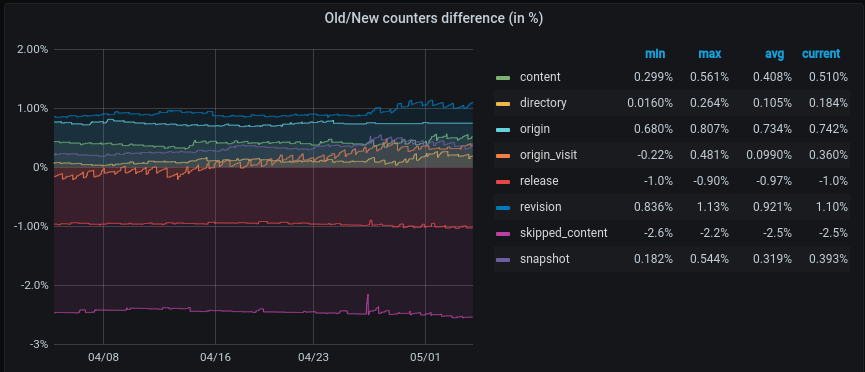
The promise is kept in terms of accuracy as most of the values have less than 1% of deviation from the reality. The only counter with a divergence greater than 1% is skipped_content with an average of 2.5% on the last month but it’s the counter with the smallest cardinality with a number of different objects less than 150 000.
The biggest counter, content, is counting more than 10 billions of unique elements with an accurracy of 0.5%.

source: grafana / SWH counters statistics

The source code of the backend is available on the archive.

This is now deployed, and you can find the up to date counters on the main archive page.

We would like to thank Éric Fusy and Frédéric Meunier for their kind help in understanding some corner cases of the algorithm, and we deeply regret that Philippe Flajolet is no longer with us to see how this is yet another application of his marvelous work in algorithms.